|
|
|
|
|
|
|
|
Liegt an der Stelle 
ein Extremum vor,
so muß gelten (notwendige Bedingung):
Die hinreichende Bedingung für ein Extremum lautet:
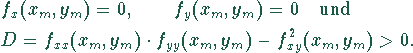
Für 
(
) liegt ein Maximum (Minimum) vor.
Geometrische Deutung:
Im Extremum besitzt die Funktion eine waagrechte
Tangentialebene.
Extremum im Dreidimensionalen (t Tangentialebene)
An einem Punkt 
, an dem die ersten partiellen
Ableitungen verschwinden, liegt ein Sattelpunkt vor, falls 
.
Auch der Sattelpunkt besitzt eine horizontale Tangentialebene.
:
, 
Mögliche Extrema bei 
und 
Überprüfung: 
, 
, 
,
,
Bei 
ist kein Extremum, da 
.
Bei 
ist 
, also ein Extremum.
Art des Extremum bei (
,0):
, an der Stelle (
,0) ist ein Maximum.
|
|
|
|
|
|
|
|
