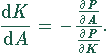Partielle Ableitungen/Produktion als Funktion von Kapitalaufwand und Arbeitsaufwand

Die Abbildung zeigt ein Produktionsgebilde.

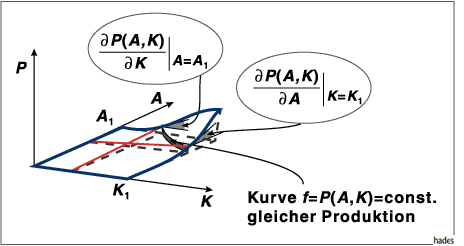
Die Produktion ist eine Funktion von zwei Faktoren z.B. Arbeitsaufwand und Kapitalaufwand.

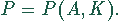
Zur Beantwortung der Frage, welcher Produktionsanteil jedem der beiden beteiligten Faktoren zuzurechnen ist, hält man jeweils den einen Faktor konstant und mißt den Einfluß des anderen durch Variation. Das entspricht den partiellen Ableitungen

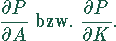
Das sind die partiellen Grenzproduktivitäten. Bei gleichzeitiger Variation sowohl des Arbeitsaufwandes als auch des Kapitaleinsatzes um infinitesimale Beträge und 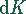ändert sich der Ertrag entsprechend dem totalen Differential

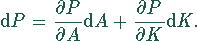
Wie müssen sich die einzelnen Faktoren ändern, damit sich der Ertrag nicht ändert?

In diesem Fall muß das totale Differential der Produktionsfunktion 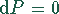sein. Das ergibt die Bestimmungsgleichung

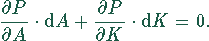
D.h., die Änderungen der beiden Faktoren A und K unterliegen der Bedingung

Dieses Verhältnis wird Substitutionsrate genannt.