Optimierung eines Produktionsverlaufes

Wir unterstellen, daß ein Angebotsmonopolist den Markt konkurrenzlos beherrscht. Seine Preis-Absatzkurve verläuft linear und ist im Bereich 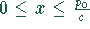definiert.

Das bedeutet, oberhalb eines Höchstpreises von 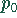ist die Ware nicht mehr absetzbar. Mit 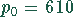und 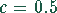lautet die Preis-Absatzfunktion

Der Gesamterlös wird durch die Funktion

bestimmt. Als Grenzerlös ergibt sich

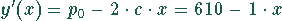
Preis und Grenzerlös sind Geraden, die die y-Achse im selben Punkt 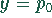schneiden.

Die Gesamterlösfunktion ist eine Parabel. Den Maximalerlös erzielt der Monopolist im Maximum der Parabel (Siehe Punkt M in der Abbildung.)

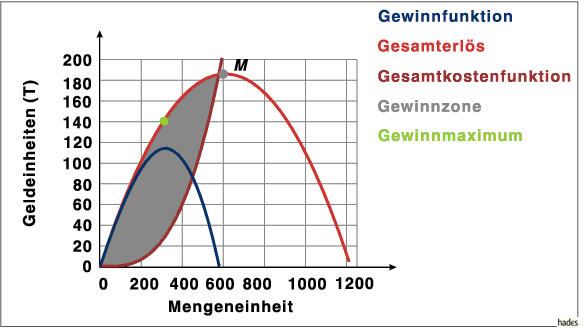
Das Ziel des Unternehmers ist aber nicht sein Maximalerlös, sondern sein maximaler Gewinn. Das ist die Differenz von Gesamterlösfunktion und Gesamtkostenfunktion. Geht man von fixen Kosten in Höhe von 500 Geldeinheiten aus und nimmt eine Gesamtkostenentwicklung nach einer kubischen Funktion

an, so ergibt sich für den Gewinn

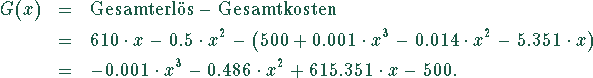
Dieser Gewinn nimmt dort sein Maximum an, wo die erste Ableitung null wird.

Dies ist eine quadratische Gleichung. Die Lösung lautet

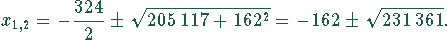
Wird das negative Vorzeichen der Wurzel verwendet, so ergibt sich für x ein negativer Wert. Eine negative Menge ist aber ökonomisch unsinnig. Es existiert also nur eine ökonomisch sinnvolle Lösung der quadratischen Gleichung

Bei einer Produktionsmenge vo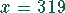n Mengeneinheiten erzielt der Monopolist einen maximalen Gewinn.