






 |
 |
 |
 |
 |
 |
 |
Formen Sie die folgenden Aufgaben in die Form 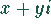 um:
um:


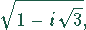

Lösung:
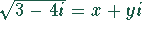 gelöst werden. Durch Quadrieren
erhält man
gelöst werden. Durch Quadrieren
erhält man
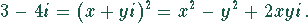
Aus dieser Gleichung ergeben sich zwei Bestimmungsgleichungen für die
Unbekannten 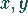 .
.
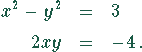
Aus der zweiten Gleichung folgt
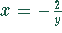 . Setzt man dies in die erste Gleichung ein, so ergibt sich eine
Gleichung 4. Grades
. Setzt man dies in die erste Gleichung ein, so ergibt sich eine
Gleichung 4. Grades
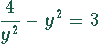
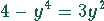
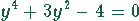
Dies ist eine biquadratische Gleichung. Als Lösung findet man
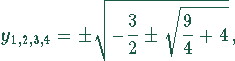
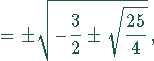
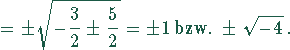
Die beiden letzten Lösungen führen zu imaginären Werten für y, die aber
per definitionem eine reelle Zahl sein soll. Deshalb bleiben als einzig mögliche
Lösungen 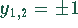 .
.
Damit ergibt sich für 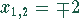 . Daraus folgt
. Daraus folgt
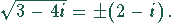
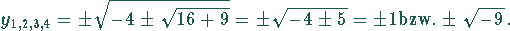
Die beiden letzten Lösungen sind wieder imaginäre Zahlen und fallen deshalb als
Lösungen aus. Die Lösungen lauten:
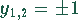 . Daraus folgen
. Daraus folgen 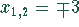 und
und
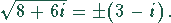
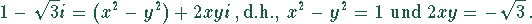
Durch Einsetzen des x-Wertes aus der zweiten Gleichung in die erste und Umformung erhält man die Gleichung 4. Grades
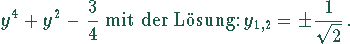
Die anderen beiden Lösungen sind imaginär. Damit wird 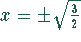 .
D.h.
.
D.h.
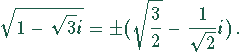


In Mathematica bzw. MapleV sind solche Aufgaben leicht zu lösen
Mathematica
z.B.
ComplexExpand[Sqrt[1-I Sqrt[3]]]
MapleV
z.B.
simplify(sqrt(1- I sqrt(3)));
