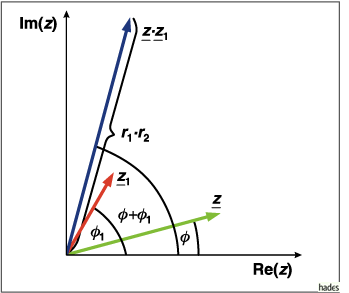
|
|
|
|
|
|
|
|
Multiplikation einer komplexen Zahl 
mit einer allgemeinen komplexen Zahl 
: 
um 
und Streckung um 
,
Diese Operationen sind
vertauschbar, man kann auch zuerst strecken und dann drehen.
Da die Multiplikation kommutativ ist, 
,
kann auch von 
ausgegangen werden.
Graphische Darstellung der Multiplikation zweier komplexer Zahlen
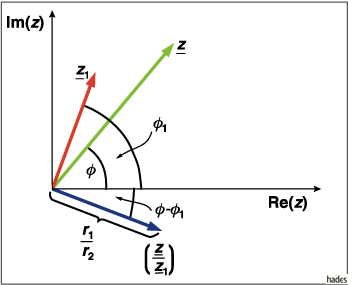
und der Division zweier komplexer Zahlen:
Division zweier komplexer Zahlen 
,
zurückführbar auf die
Multiplikation:
Streckung des Zeigers 
um das 
-fache,
Drehung um 
.
Division von z durch die imaginäre Einheit 
entspricht einer Drehung von 
um 
,
.
|
|
|
|
|
|
|
|
