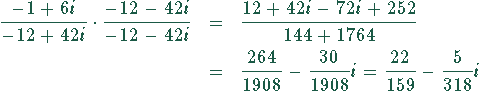|
 |
 |
 |
 |
 |
 |
Man stelle die komplexen Zahlen in der Form 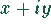 dar.
dar.
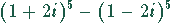
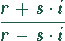
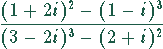
Lösung
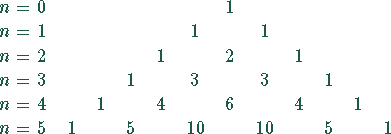
Damit ergibt sich für den ersten bzw. zweiten Summanden
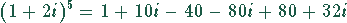
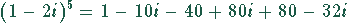
Zieht man den zweiten von dem ersten Summanden ab, ergibt sich
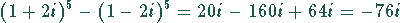
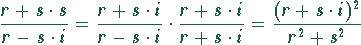
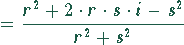
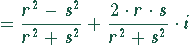
Zähler:
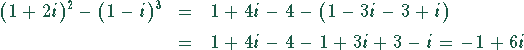
Nenner:
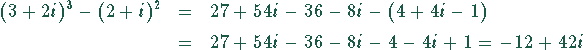
Das ergibt
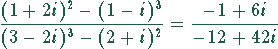
Jetzt muß wieder der Nenner zu einer reellen Zahl gemacht werden, was durch Multiplikation mit der konjugierten komplexen Größe geschieht. Damit sich der Bruch nicht ändert, muß man auch den Zähler mit dieser Größe multiplizieren.