|
|
|
|
|
|
|
|
Die Wildschweinpopulation 
in einem ausgedehnten Waldstück wächst proportional
zu seinem Bestand mit einer Wachstumsrate 
. Diese Wachstumsrate
enspricht der Selbstreproduktion ohne äußere Einflüsse. Dies führt zu einer
homogenen linearen Differentialgleichung erster Ordnung
Die Lösung dieser Differentialgleichung führt auf ein lineares Wachstumsgesetz für diese Wildschweinpopulation
Wird diese Wildschweinpopulation durch äußere Einflüsse, z.B. mit einer konstanten Abschußrate a, beeinflußt, so führt dies auf eine inhomogene lineare Differentialgleichung erster Ordnung
Die Lösung führt auf die Population
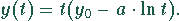
Die Festlegung einer Abschußrate führt dazu, daß die Population nach der Zeit
ausgestorben ist.
