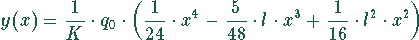|
 |
 |
 |
 |
 |
 |
Ein Balken ist einseitig eingespannt. Das andere Ende liegt frei auf einem Lager.
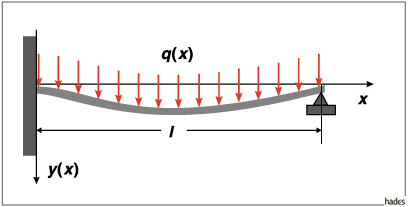
Für die Balkendurchbiegung gilt bei konstanter Biegesteifigkeit K
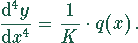
Unter der Annahme einer zur Balkenachse 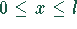 konstant wirkenden
Streckenlast
konstant wirkenden
Streckenlast 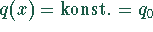 kann die Differentialgleichung 4. Ordnung direkt
integriert werden. Das ergibt
kann die Differentialgleichung 4. Ordnung direkt
integriert werden. Das ergibt
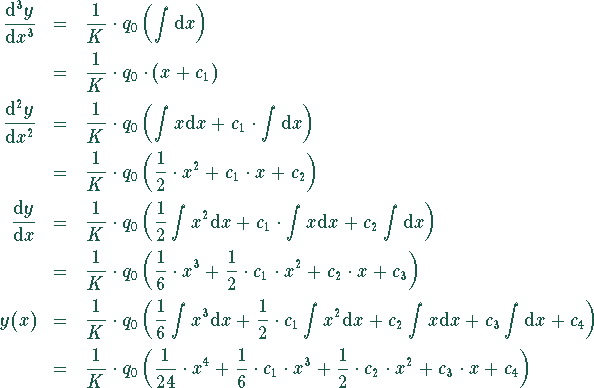
Die Randbedingungen bestimmen die Integrationskonstanten. Da der Balken bei  eingespannt ist, folgt
eingespannt ist, folgt
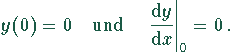
Die Lagerung des Balkens bei 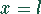 fordert
fordert

Aus diesen Randbedingungen ergeben sich, daß die Integrationskonstanten
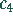 und
und 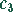 identisch null sein müssen:
identisch null sein müssen:

Für die Integrationskonstanten 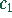 und
und 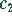 lassen sich die Bestimmungsgleichungen
ableiten:
lassen sich die Bestimmungsgleichungen
ableiten:
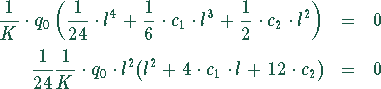
und
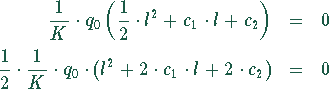
Das sind zwei Gleichungen für die zwei Unbekannten 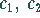 . Zur Lösung
kann die CRAMERsche Regel verwendet werden. Die Bedingungen werden erfüllt,
wenn die Klammerausdrücke null werden. In Matrizen-Schreibweise lauten die
Bestimmungsgleichungen
. Zur Lösung
kann die CRAMERsche Regel verwendet werden. Die Bedingungen werden erfüllt,
wenn die Klammerausdrücke null werden. In Matrizen-Schreibweise lauten die
Bestimmungsgleichungen
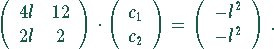
Es gilt
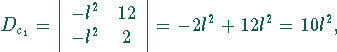
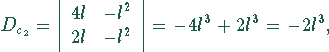
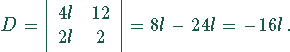
Damit ergeben sich als Lösungen
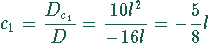
und
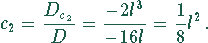
Die Lösung für die Balkendurchbiegung ist