Verteilungsfunktion/Gütekontrolle

Die Güte eines Garnes hängt von der Reißfestigkeit ab. Zwei Produzenten stellen das gleiche Garn her. Der Produzent A gibt als mittlere Reißfestigkeit MPa und der Produzent B dagegen nur MPa an. Die Reißfestigkeit eines Garnes ist, bedingt durch unkontrollierbare Produktionseinflüsse, eine normalverteilte Größe. Die Varianz beim Produzenten A beträgt 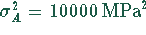gegenüber 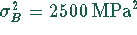beim Produzenten B. Die Toleranzgrenze beträgt 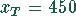MPa. Welches Garn ist besser?

Oberflächlich betrachtet scheint das Garn des Produzenten mit der größeren mittleren Reißfestigkeit am besten zu sein. Berechnet man aber die Verteilungsfunktion für die Toleranzgrenze, so findet man für den Produzenten A , daß ca. 24 % der Produktion unterhalb der Toleranzgrenze liegt, während beim Produzenten B nur ca. 16 % unterhalb der Toleranzgrenze liegt. In der Abbildung wird dies verdeutlicht.

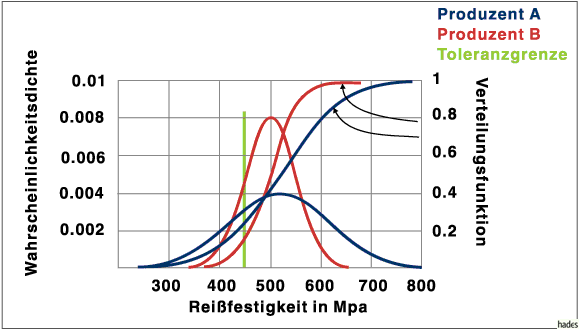
Mit Hilfe von Mathematica läßt sich dies leicht nachprüfen:

Mathematica

Needs["Statistics`Master`"]
verteil=NormalDistribution[mu, sigma]
mu=520
sigma=100
CDF[verteil,450]
y1=Plot[PDF[verteil,x],{x,200,800}]
y2=Plot[0.01 CDF[verteil,x],{x,200,800}]
mu=500
sigma=50
CDF[verteil,450]
y3=Plot[PDF[verteil,x],{x,200,800}]
y4=Plot[0.01 CDF[verteil,x],{x,200,800}]

Der Faktor von 0.01 bei den Darstellungen y2 und y4 ist lediglich als Maßstabsänderung eingeführt, um die Verteilungsfunktion und die Wahrscheinlichkeitsdichten in einer Abbildung darstellen zu können.

MapleV

>with(stats):
>plot(N(x,520,10000),x=200..800);
>plot(diff(N(x,520,10000),x),x=200..800);
>plot(N(x,500,2500),x=200..800);
>plot(diff(N(x,500,2500),x),x=200..800);
>N(450,520,10000);
>N(450,500,2500);

Achtung!! Im Gegensatz zum Taschenbuch steht in Maple im Nenner des Exponenten der Wahrscheinlichkeitsdichte nicht 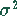, sondern . Deshalb steht in dem obigen Programm für MapleV statt 100 der Wert des Quadrates 10000. Dasselbe gilt für den Produzenten B (50, d.h. 2500).