|
|
|
|
|
|
|
|
Es soll die optimale Nutzungsdauer einer Maschine mit dem Anschaffungswert
von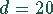 
TDM ermittelt werden. Die bisherigen Reparaturkosten 
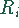in TDM in den Jahren 
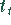sind in der Tabelle zusammengefaßt.
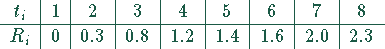
Folgende Bezeichnungen werden verwendet:
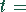Nutzungsdauer
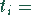Nutzungszeit
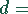abzuschreibender Betrag (Anschaffungswert)
Dann sind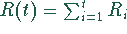 
die Reparaturkosten während der Nutzungsdauer
t. Die mittleren Kosten pro Nutzungszeiteinheit betragen dann
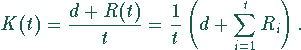
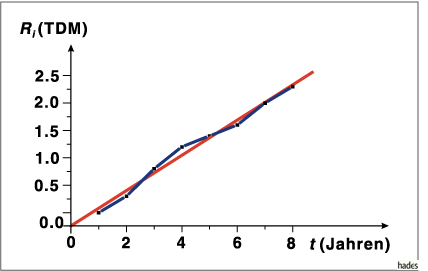
Die Reparaturkosten lassen sich mittels einer Trendfunktion aus den bisher angefallenen Kosten berechnen. In der Abbildung sind die bisher angefallenen Reparaturkosten dargestellt.
Offensichtlich kann man die Trendfunktion für die Reperaturkosten durch eine Gerade annähern
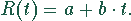
Die Parameter a und b lassen sich mittels der linearen Regression bestimmen. Dazu kann entweder das Pascal-Programm des Taschenbuches benutzt werden, oder man benutzt Mathematikprogramme wie Mathematica oder MapleV. Die Befehlsfolgen sind:
Mathematica
Fit[{0,0.3,0.8,1.2,1.4,1.6,2.0,2.3},{1,x},x]
MapleV
with(stats): linregress([0,0.3,0.8,1.2,1.4,1.6,2.0,2.3],[1,2,3,4,5,6,7,8]);Man erhält
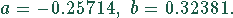
Die Kostenfunktion kann unter der Annahme einer linearen Abhängigkeit der
Trendfunktion für die Reparaturkosten weiter berechnet werden.
Dazu wird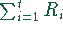 
benötigt:
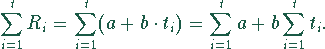
Es gilt
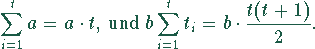
Die letzte Formel entsteht aus der Summenformel für die arithmetische Reihe. Das ergibt für die Kostenfunktion
Für das Optimum (minimale Kosten) muß gelten
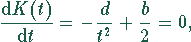
woraus
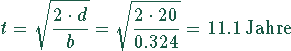
folgt.
Nach 11 Jahren ist die Maschine aus dem Arbeitsprozeß auszusondern.
