






 |
 |
 |
 |
 |
 |
 |
Für die lineare Optimierung liefert MapleV das Packet 'simplex'. Die Syntax lautet:
with(simplex) minimize(Zielfunktion, Einschränkungen in Form von Ungleichungen mit <= bzw.>=); maximize(Zielfunktion, Einschränkungen in Form von Ungleichungen mit <= bzw.<=);
Beispiel:
Es werden die Produkte 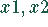 auf den Maschinen
auf den Maschinen 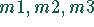 produziert. die
Gewinnfunktion ist
produziert. die
Gewinnfunktion ist
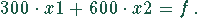
Die Produktionszeit/Monat auf den Maschinen beträgt:
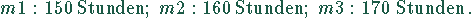
Das Produkt 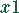 benötigt auf den Maschinen
benötigt auf den Maschinen 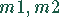 je 3 Stunden. Das Produkt
je 3 Stunden. Das Produkt
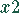 benötigt auf der Maschine
benötigt auf der Maschine 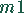 2 Stunden, auf der Maschine
2 Stunden, auf der Maschine 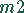 4 Stunden
und auf der Maschine
4 Stunden
und auf der Maschine 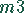 6 Stunden. Daraus ergibt sich folgende Optimierung:
6 Stunden. Daraus ergibt sich folgende Optimierung:
with(simplex):
f:=300*x1+600*x2:
einschr1:=3*x1+2*x2<=150:
einschr2:=3*x1+4*x2<=160:
einschr3:=6*x2<=170:
maximize(f,{einschr1,einschr2,einschr3});
evalf(");
Ein Beispiel für Transportprobleme:
Ein Transportunternehmen hat drei Milchwerke (m1,m2,m3) mit Milch von drei Rinderställen (r1,r2,r3) zu beliefern. Der tägliche Bedarf beträgt 1000 l, 2000 l bzw. 2500 l. Die Rinderställe haben eine Tageskapazität von 800 l, 1500 l, 2300 l.
Die Transportkosten pro 1 Liter Milch in DM sind in der folgenden Tabelle aufgeführt:
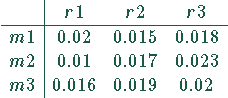
Die Gesamtkosten sollen minimiert werden.
Es existieren neun Variable (x[1][1], x[1][2] usw. bis x[3][3]), da jedes Milchwerk von jedem Rinderstall beliefert werden kann. Die zu minimierende Größe ist
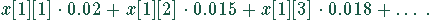
Die Einschränkungen sind einmal durch die Kapazität der Milchwerke gegeben:
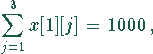
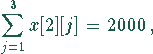
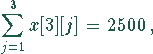
und zum anderen durch die Kapazität der Rinderställe bestimmt:
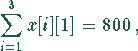
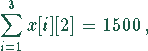
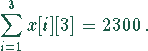
In MapleV läßt sich dieses Problem wie folgt lösen:
restart:
with(simplex):
ri:=[1700,1500,2300]:
mi:=[1000,2000,2500]:
kosten:=array([[0.02,0.015,0.018],[0.01,0.017,0.023],[0.016,0.019,0.02]]);
x:=array(1..3,1..3):
r := {seq(sum(x[i,'j'],'j'=1..3)=ri[i],i=1..3)} union
{seq(sum(x['i',j],'i'=1..3)=mi[j],j=1..3)};
v:={seq(seq(x[i,j],i=1..3),j=1..3)}:
z:={}:
for i from 1 to 3 do
for j from 1 to 3 do
z:=z union{x[i,j]*kosten[i,j]}:
od;
od;
z:=convert(z,`+`);
minimize(z,r,NONNEGATIVE);
assign("); eval(x);
z;
Dieses Beispiel kann leicht auf mehr Quellen und Zielorte erweitert werden.
