Divergenz

Kartesisches Koordinatensystem:

Remove["Global`*"]
Needs["Calculus`VectorAnalysis`"]
SetCoordinates[Cartesian]
vektorf[x_,y_,z_]:={fx[x,y,z],fy[x,y,z],fz[x,y,z]}
Div[vektorf[x,y,z]]

Beispiel:

Für ein Vektorfeld

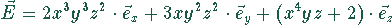
ist die Divergenz zu bilden:

Remove["Global`*"]
Needs["Calculus`VectorAnalysis`"]
SetCoordinates[Cartesian]
fx[x,y,z]=2 x^3 y^3 z^2; fy[x,y,z]=3 x y^2 z^2;fz[x,y,z]=x^4 y z+2
vektorf[x_,y_,z_]:={fx[x,y,z],fy[x,y,z],fz[x,y,z]}
Div[vektorf[x,y,z]]

Sphärische Koordinaten:

Ein Dipol der Dipolstärke 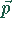erzeugt am Punkt r ein elektrisches Feld

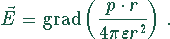
Das liefert die Divergenz:

Remove["Global`*"]
Needs["Calculus`VectorAnalysis`"]
SetCoordinates[Spherical]
pot=p Cos[theta]/(2 Pi eps r^2);
efeld[r_,theta_,phi_]= Grad[pot]
quelle=Div[efeld[r,theta,phi]]