|
|
|
|
|
|
|
|
Divergenz oder Quelle eines Feldes 
im Punkt 
ist die
Bilanz des durch die Oberfläche 
eines infinitesimal kleinen Volumens 
um den Punkt 
gehenden Vektorflusses 
, d.h. die Differenz zwischen
Zufluß und Abfluß:
(
ist der auf dem Flächenelement senkrecht stehende Normalenvektor).
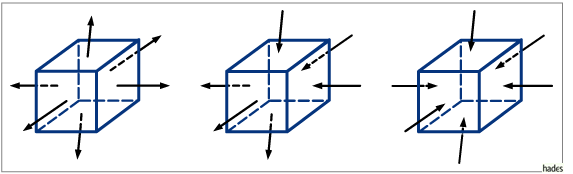
Schematische Flußdarstellung zu div
,
div
und div
.
Divergenz von 
am Ursprung in einem kleinen Kugelvolumen
mit Radius R
Das Quellfeld div
kann als Skalarprodukt des 
-
Differentialoperators mit einem Vektorfeld 
aufgefaßt werden
und ist daher ein skalares Feld.
In der Elektrostatik ist die Divergenz des elektrischen Feldes
(Vektorfeld) gleich der dem (skalaren) Dichtefeld 
der
Ladungen.
Ergiebigkeit eines Volumens 
ist 
.
|
|
|
|
|
|
|
|
