|
|
|
|
|
|
|
|
Remove["Global`*"]
Needs["Calculus`LaplaceTransform`"]
dgl=a y''[t]+b y'[t]+c y[t]==f[t]
(* Lineare Differentialgleichung einer Funktion y(t) *)
a= (* Parameter eingeben *)
b= (* Parameter eingeben *)
c= (* Parameter eingeben *)
f[t]:= (* Inhomgenitaet *)
dgl
y0= ; (* Randbedingungen bzw. Anfangsbedingungen y(0) *)
y10= ; (* Randbedingungen bzw. Anfangsbedingungen y'(0) usw.*)
LaplaceTransform[dgl,t,s]
% /. {y[0]->y0,y'[0]->y10, LaplaceTransform[y[t],t,s]->yl[s]}
Solve[%,yl[s]]
y[ t_] =InverseLaplaceTransform[yl[s] /. %[[1]],s,t]
(* Graphische Darstellung der Lösung *)
Plot[y[t],{t,0,10}]
Beispiel: Stromkreis mit Widerstand, Spule und Kondensator (siehe auch
Beispiel 2 , Induktivität 
Henry, Widerstand 
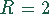Ohm, Kapazität 
Farad)
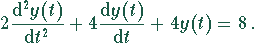
Remove["Global`*"]
Needs["Calculus`LaplaceTransform`"]
dgl=a y''[t]+b y'[t]+c y[t]==f[t]
(* Lineare Differentialgleichung einer Funktion y(t) *)
a:= 2 ;
b:= 4 ;
c:= 4 ;
f[t]:= 8 ;
dgl
y0= 0 ; (* Randbedingungen bzw. Anfangsbedingungen y(0) *)
y10= 0 ; (* Randbedingungen bzw. Anfangsbedingungen y'(0) usw.*)
LaplaceTransform[dgl,t,s]
% /. {y[0]->y0,y'[0]->y10, LaplaceTransform[y[t],t,s]->yl[s]}
Solve[%,yl[s]]
y[ t_] =InverseLaplaceTransform[yl[s] /. %[[1]],s,t]
(* Graphische Darstellung der Lösung *)
Plot[y[t],{t,0,10},PlotRange->{{0,10},{0,2.5}}]
