Bernstein-Polynome
Bernstein-Polynome: Polynome vom Grad n:


Sie werden nur im Bereich  verwendet und haben dort
folgende Eigenschaften:
verwendet und haben dort
folgende Eigenschaften:
- eine k-fache Nullstelle bei
 ,
,
- eine
 -fache Nullstelle bei
-fache Nullstelle bei  ,
,
- genau ein Maximum bei
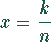 ,
,
- alle Polynome eines Grades bilden eine Zerlegung der Eins,
d.h.
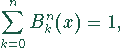
- die Polynome
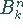 sind linear unabhängig und bilden eine Basis
für Polynome vom Höchstgrad n, d.h., alle Polynome n-ten Grades
können als Linearkombination von Bernstein-Polynomen beschrieben
werden,
sind linear unabhängig und bilden eine Basis
für Polynome vom Höchstgrad n, d.h., alle Polynome n-ten Grades
können als Linearkombination von Bernstein-Polynomen beschrieben
werden,
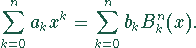















![]()

![]() verwendet und haben dort
folgende Eigenschaften:
verwendet und haben dort
folgende Eigenschaften:
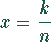 ,
,
![]()
![]()







