|
|
|
|
|
|
|
|
Nachdem in der Darstellung von f eventuelle gemeinsame Linearfaktoren von Zähler
und Nenner gekürzt wurden gilt:
Die Funktion 
besitzt die Nullstellen des Zählerpolynoms 
als Nullstellen und die Nullstellen des Nennerpolynoms 
als
Polstellen.
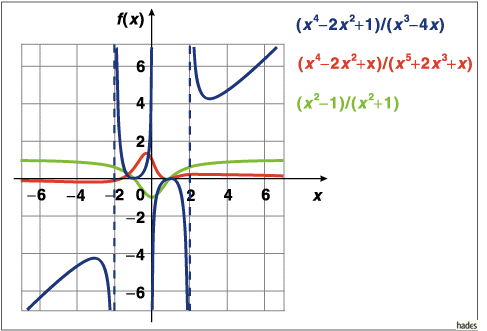
Mathematica Code:
Plot[{((x^4-2(x^2)+1)/(x^3-4x)),((x^4-2(x^2)+1)/(x^5+x^3-2x)),
((x^4-2(x^2)+x)/(x^5+2(x^3)+x)),(x^2-1)/(x^2+1)},{x,-7,7}, PlotRange->{{-7,7},{-7,7}},
PlotStyle->{{Hue[0]},{Hue[0.3]},{Hue[0.6]},{Hue[0.8]}}, AspectRatio->Automatic]
Besitzen Zähler und Nenner am gleichen Punkt 
eine Nullstelle
der gleichen Ordnung, so kann die Definitionslücke an diesem
Punkt stetig behoben werden.
Ist die Nullstelle des Zählers von höherer Ordnung als die
Nullstelle des Nenners, so ist die stetige Erweiterung eine Nullstelle
der Funktion.
bestimmt.
|
|
|
|
|
|
|
|
