Wurzel rationaler Funktionen - Grafische Darstellung
Die Funktion 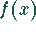 wird im wesentlichen durch das Verhalten von
wird im wesentlichen durch das Verhalten von
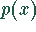 und
und 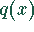 bestimmt.
bestimmt.
Die Nullstellen von 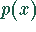 sind die Nullstellen von
sind die Nullstellen von 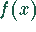 und die
Nullstellen von
und die
Nullstellen von 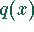 sind die Polstellen von
sind die Polstellen von 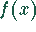 .
.
 Haben Zähler und Nennerpolynom an der gleichen Stelle
Haben Zähler und Nennerpolynom an der gleichen Stelle 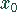 eine Nullstelle, so ist auf den Grad der Nullstellen zu achten, um zu
entscheiden, ob es sich um einen Pol oder um eine
hebbare Lücke handelt.
eine Nullstelle, so ist auf den Grad der Nullstellen zu achten, um zu
entscheiden, ob es sich um einen Pol oder um eine
hebbare Lücke handelt.
 Die Funktion ist nur dort definiert, wo
Die Funktion ist nur dort definiert, wo 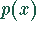 und
und 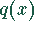 gleiches
Vorzeichen haben.
gleiches
Vorzeichen haben.
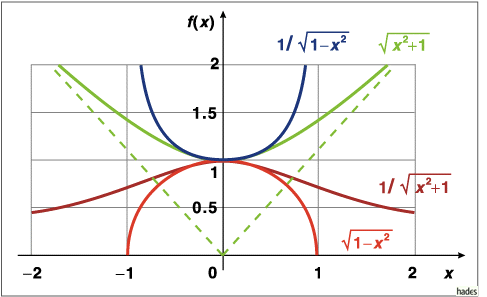
Mathematica Code:
Plot[{Sqrt[1-x^2],Sqrt[x^2+1],1/Sqrt[1-x^2],1/Sqrt[x^2+1]},{x,-2,2}, PlotRange->{{-2,2},{0,2}},
PlotStyle->{{Hue[0]},{Hue[0.3]},{Hue[0.6]},{Hue[0.8]}}, AspectRatio->Automatic]
Die Funktion 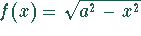 beschreibt die obere Hälfte
eines Kreises mit Radius
beschreibt die obere Hälfte
eines Kreises mit Radius 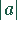 .
.
Ihre reziproke Funktion hat ein Minimum bei  und divergiert
bei
und divergiert
bei 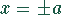 .
.
Die Funktion 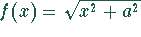 beschreibt den positiven Arm
einer Hyperbel mit den Asymptoten
beschreibt den positiven Arm
einer Hyperbel mit den Asymptoten 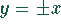 .
.
Ihre reziproke Funktion hat ein Maximum bei  und geht für
und geht für
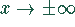 gegen Null.
gegen Null.















 Haben Zähler und Nennerpolynom an der gleichen Stelle
Haben Zähler und Nennerpolynom an der gleichen Stelle  Die Funktion ist nur dort definiert, wo
Die Funktion ist nur dort definiert, wo 







