Wurzel rationaler Funktionen - Spezielle Erweiterungen und Anwendungen
Komplexe Argumente: Wie bei den Wurzelfunktionen beschrieben,
kann die Wurzel auch für komplexe Argumente definiert werden.
Interessanter Spezialfall: für rein imaginäres Argument 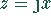 vertauschen die beiden Beispielfunktionen ihre anschauliche Deutung:
vertauschen die beiden Beispielfunktionen ihre anschauliche Deutung:
 Die Funktion
Die Funktion 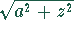 stellt einen Kreisbogen dar:
stellt einen Kreisbogen dar:
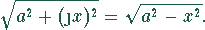
 Die Funktion
Die Funktion 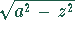 stellt einen Hyperbelbogen dar:
stellt einen Hyperbelbogen dar:
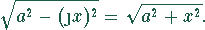
 Mit dieser anschaulichen Darstellung lassen sich die Zusammenhänge
zwischen trigonometrischen und hyperbolischen Funktionen im Komplexen
aufgrund der geometrischen Deutung dieser Funktionen
besser verstehen.
Mit dieser anschaulichen Darstellung lassen sich die Zusammenhänge
zwischen trigonometrischen und hyperbolischen Funktionen im Komplexen
aufgrund der geometrischen Deutung dieser Funktionen
besser verstehen.















 Die Funktion
Die Funktion ![]()
 Die Funktion
Die Funktion ![]() stellt einen Hyperbelbogen dar:
stellt einen Hyperbelbogen dar:
![]()
 Mit dieser anschaulichen Darstellung lassen sich die Zusammenhänge
zwischen trigonometrischen und hyperbolischen Funktionen im Komplexen
aufgrund der geometrischen Deutung dieser Funktionen
besser verstehen.
Mit dieser anschaulichen Darstellung lassen sich die Zusammenhänge
zwischen trigonometrischen und hyperbolischen Funktionen im Komplexen
aufgrund der geometrischen Deutung dieser Funktionen
besser verstehen.






