Hyperboloid

a, b: Länge der reellen Halbachsen, c: Länge der imaginären Halbachse. 

Geradlinige Erzeugende einer Fläche:   Gerade, die ganz in der Fläche liegt.

Die zwei Erzeugenden des einschaligen Hyperboloides:

wobei u und v beliebige Größen sind. Durch jeden Flächenpunkt gehen jeweils zwei erzeugende Geraden hindurch.

Zweischaliges Hyperboloid, 

c: Länge der reellen Halbachse, a, b: Länge der imaginären Halbachsen.

Schnitte parallel zur z-Achse sind bei beiden Hyperboloiden wieder Hyperbeln (für das einschalige Hyperboloid sind auch zwei sich schneidende Geraden möglich),
Schnitte parallel zur -Ebene sind Ellipsen.

Rotationshyperboloid:  für den Fall , entsteht durch Rotation einer Hyperbel mit den Halbachsen a und c um die Achse .

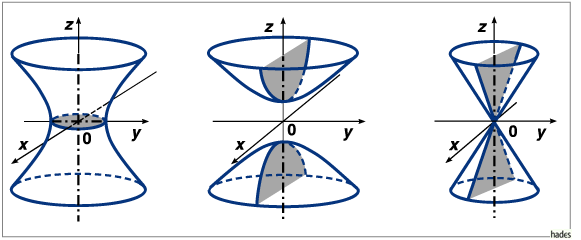
Einschaliges Hyperboloid, zweischaliges Hyperboloid und reeller Kegel.