|
|
|
|
|
|
|
|
.
Flächeninhalt des Parallelogramms
der Grundfläche:
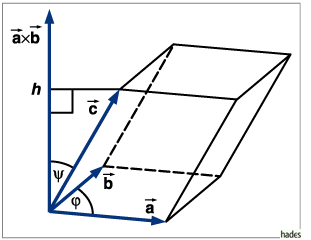
Höhe, Länge der Projektion des Vektors 
auf
:
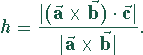
Spatvolumen (Grundfläche multipliziert mit der Höhe):
Das Spatprodukt (das Volumen des von den drei Vektoren aufgespannten Spates)
dreier linear abhängiger Vektoren
(komplanare Vektoren)
ist gleich Null.
Volumen eines Tetraeders:
Orientiertes Spatvolumen 
mit
Vorzeichen läßt sich definieren, wenn man die Betragsstriche
des Sinus wegläßt, 
bilden
ein Linkssystem.
|
|
|
|
|
|
|
|
