|
|
|
|
|
|
|
|
Symmetrische Matrizen sind spiegelsymmetrisch zu ihrer
Hauptdiagonalen, es gilt
Symmetrische Matrix:
Antisymmetrische oder
schiefsymmetrische Matrix, eine quadratische Matrix,
die dem Negativen ihrer
Transponierten gleich ist:
Für antisymmetrische
Matrizen gilt 
, alle Diagonalelemente sind gleich null
. Somit verschwindet auch die Spur: 
.
Antisymmetrische Matrix:
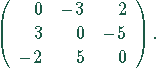
Jede quadratische Matrix kann in eine Summe aus einer
symmetrischen 
und einer antisymmetrischen Matrix
zerlegt werden 
, mit:
Zerlegung einer quadratischen Matrix in eine Summe einer
symmetrischen und
einer antisymmetrischen Matrix:
|
|
|
|
|
|
|
|
