Minimale Überdeckung
Es sind nicht immer alle gefundene Primimplikanten nötig,
um die Funktion darzustellen.
Die benötigten Primimplikanten werden bestimmt durch den
Algorithmus zur Bestimmung der minimalen Überdeckung:
- Erstelle eine neue Tabelle. Markiere die Spalten mit
den Konjunktionstermen. Die Zeilen werden mit den Primimplikanten
bezeichnet. Dabei werden die Primimplikanten nach
aufsteigender Länge sortiert.
- Trage in die Kreuzungsfelder aller Zeilen und Spalten ein
 ein, wenn der zugehörige Konjunktionsterm Implikant des
zugehörigen Primimplikanten ist.
ein, wenn der zugehörige Konjunktionsterm Implikant des
zugehörigen Primimplikanten ist.
- Streiche alle Zeilen und Spalten aus der Tabelle, für die
gilt, die Spalte enthält nur ein
 .
Der zugehörige Primimplikant ist nötig und wird notiert.
Wiederhole diesen Schritt, bis keine Spalte mehr ein
einzelnes
.
Der zugehörige Primimplikant ist nötig und wird notiert.
Wiederhole diesen Schritt, bis keine Spalte mehr ein
einzelnes  enthält.
enthält.
- Wähle Zeilen aus der Tabelle, so daß
eine neue Tabelle entsteht, mit folgenden Eigenschaften:
1. Jede Spalte enthält wenigstens ein  .
.
2. Die Summe der Primimplikantenlängen
ist möglichst klein.
- Alle Primimplikanten der neuen Tabelle werden als nötige
Primimplikanten notiert.
- Die disjunktive Verknüpfung aller nötigen Primimplikanten
stellt die gesuchte minimale Funktion dar.
 Die Konjunktionsterme und Primimplikanten
des vorigen Beispiels bilden folgende Tabelle:
Die Konjunktionsterme und Primimplikanten
des vorigen Beispiels bilden folgende Tabelle:
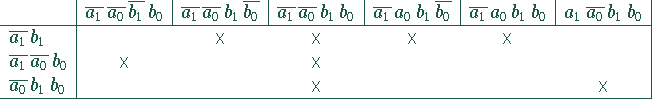
Bis auf die dritte Spalte enthalten alle Spalten genau
ein  . Es werden daher alle Zeilen gestrichen
und alle Primimplikanten in die Liste der nötigen
Primimplikanten aufgenommen.
. Es werden daher alle Zeilen gestrichen
und alle Primimplikanten in die Liste der nötigen
Primimplikanten aufgenommen.
Die minimale Funktion lautet
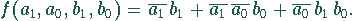















 Die Konjunktionsterme und Primimplikanten
des vorigen Beispiels bilden folgende Tabelle:
Die Konjunktionsterme und Primimplikanten
des vorigen Beispiels bilden folgende Tabelle:
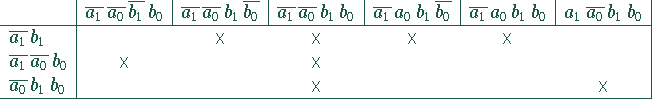
![]() . Es werden daher alle Zeilen gestrichen
und alle Primimplikanten in die Liste der nötigen
Primimplikanten aufgenommen.
. Es werden daher alle Zeilen gestrichen
und alle Primimplikanten in die Liste der nötigen
Primimplikanten aufgenommen.![]()







