|
|
|
|
|
|
|
|
Multiplikation einer 
-Matrix 
mit einem n-dimensionalen Spaltenvektor 
ergibt
einen
Spaltenvektor 
mit m Zeilen (Komponenten):
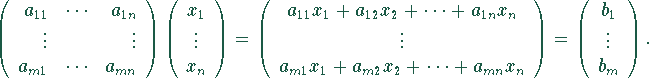
Dies ist die Kurzschreibweise für lineare
Gleichungssysteme, 
heißt Systemmatrix, 
Konstantenvektor, 
Lösungs- oder Systemvektor.
Die Komponenten 
erhält man als Skalarprodukt zwischen den
Zeilenvektoren 
der Matrix 
und dem Vektor
:
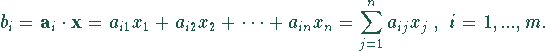
Multiplikation einer Matrix mit einem Vektor:
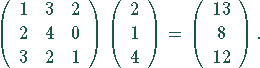
Das Produkt der Matrix 
mit der Vektor
ist nur definiert, wenn 
genau so viele
Spalten wie 
Zeilen (Komponenten) hat.
|
|
|
|
|
|
|
|
