|
|
|
|
|
|
|
|
von zwei drei-komponentigen Vektoren 
und
, gekennzeichnet durch ein Kreuz zwischen den Vektoren, ergibt einen Vektor.
Dyadisches Produkt
oder tensorielles Produkt, Produkt zweier
Vektoren 
mit m Elementen und 
mit n
Elementen, das eine 
-Matrix ergibt. Die Elemente 
der Dyade 
aus den Vektoren 
und 
sind
gegeben durch:
Das dyadische Produkt kann als Matrixprodukt (siehe
Multiplikation von Matrizen) definiert werden:
: Matrix mit einer Spalte (= Spaltenvektor).
: Matrix mit einer Zeile (= Zeilenvektor).
Dyadisches Produkt:
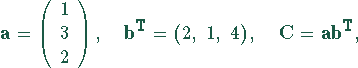
Das dyadische Produkt aus dem Vektor 
mit
mit sich selbst (
Matrixprodukt von 
mit 
) ergibt die quadratische symmetrische 
-Matrix:
die als Matrixelemente alle möglichen Produkte der Zahlen von 
bis 
enthält, also das kleine Einmaleins:
|
|
|
|
|
|
|
|
