|
|
|
|
|
|
|
|
Linearkombinationsregel:
Der Wert der Determinante ändert sich nicht, wenn man zu
einer Zeile bzw. Spalte ein beliebiges Vielfaches der anderen
Zeile bzw. Spalte elementweise addiert oder subtrahiert.
Multiplikationsatz für Determinanten:
Die Determinante des Matrixproduktes zweier
Matrizen 
und 
ist gleich
dem Produkt der Determinanten der einzelnen Matrizen:
Das Multiplikationstheorem liefert eine Möglichkeit,
die Determinante eines Matrixproduktes direkt aus den Determinanten der
einzelnen Matrizen zu berechnen. Die Berechnung des
Matrixproduktes kann man sich so sparen.
Zerlegungssatz, besteht eine Zeile (oder Spalte) aus
einer Summe von Elementen, so kann die Determinante
folgendermaßen in eine Summe von zwei Determinanten zerlegt
werden:
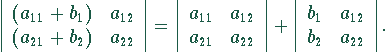
Determinante von Dreiecksmatrizen,
die Determinante einer Dreiecksmatrix ist gleich dem Produkt der
Hauptdiagonalelemente und besitzt
den Wert:
Determinante der Diagonalmatrix
(gleichzeitig obere und untere
Dreiecksmatrix):
Für die Einheitsmatrix gilt analog: 
.
Für die Nullmatrix gilt: 
|
|
|
|
|
|
|
|
