Definition von Mehrfachintegralen

Doppelintegral,  Grenzübergang einer Doppelsumme über Flächenbereiche über eine Funktion von zwei unabhängigen Variablen (Integral in zwei Dimensionen), analog zum einfachen Integral definiert:

Flächendifferential, 

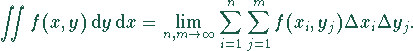
Doppelintegral setzt sich aus äußerem und innerem Integral zusammen. Es wird durch zwei aufeinanderfolgende gewöhnliche Integrationen berechnet.

In Polarkoordinaten lautet das Flächendifferential :

Dreifachintegral,  berechnet man durch drei aufeinanderfolgende gewöhnliche Integrationen. Je nach Form des zu integrierenden Volumens wählt man entsprechend angepaßte Koordinaten bzw. passende Volumenelemente.  

 
Volumen einer Kugel:
.