Zurück Vor +Ebene Home Inhalt Index Hilfe

Singuläre Punkte

Singuläre Punkte:
a) Doppelpunkte, in denen sich die Kurve selbst schneidet;
b) Isolierte Punkte,  die außerhalb der Kurve liegen;
c) Rückkehrpunkte,  in denen sich der Durchlaufsinn der Kurve ändert (gleiche Tangenten);
d) Berührungspunkte,  in denen sich die Kurve selbst berührt;
e) Knickpunkte,  in denen die Kurve sprunghaft die Richtung ändert (unterschiedliche Tangenten);
f) Asymptotische Punkte,  um die sich die Kurve unendlich herumwindet.

Ermittlung von singulären Punkten der Art a) bis d):

Untersuchung der Kurve in der Form ,
Notwendige Bedingungsgleichung:

und mindestens eine der drei Ableitungen zweiter Ordnung verschwindet nicht:

Eigenschaft des mehrfachen Punktes hängt ab vom Vorzeichen von

1) : Isolierter Punkt;
2) : Rückkehrpunkt oder Berührungspunkt, Steigung der Tangente

3) : Doppelpunkt, Steigung der Tangenten m aus


 
Andere Darstellungsarten in die implizite Darstellung umformen.
 
:

aber nur der erste Punkt liegt auf der Kurve!
isolierter Punkt.
 

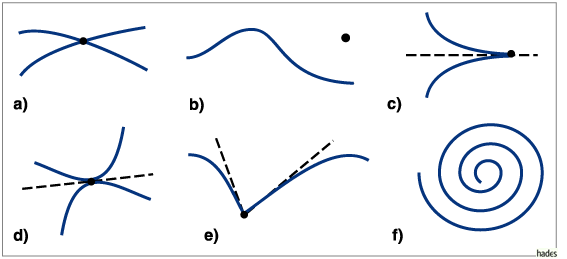
Singuläre Punkte

Zurück Vor +Ebene Home Inhalt Index Hilfe

Copyright Verlag Harri Deutsch AG Stöcker DeskTop Mathematik