|
|
|
|
|
|
|
|
Eine Funktion 
heißt in 
differenzierbar,
wenn für alle Folgen, die zu 
konvergieren, der Grenzwert
existiert, d.h. endlich ist.
Stimmen linksseitige Ableitung
überein, so ist die Funktion an der Stelle 
differenzierbar.
Notwendige - aber nicht hinreichende - Bedingung für
Differenzierbarkeit einer Funktion ist ihre Stetigkeit an dieser
Stelle.
Differenzierbare Funktionen sind anschaulich
,,glatte`` Kurven.
Eine Funktion ist in einem Punkt nicht differenzierbar, wenn sie
dort unstetig ist. Weist die Kurve einen Knick auf, dann
existieren nur die linksseitige und rechtsseitige Ableitung, d.h. die
Steigung der Tangente ändert sich an der Knickstelle sprunghaft.
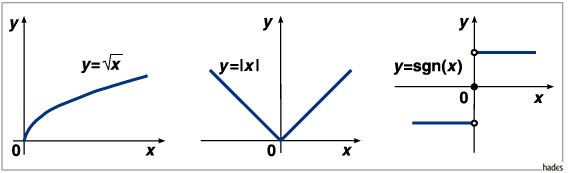
Nicht differenzierbare Funktionen in 
: links
Wurzel-, Mitte Betrags-, rechts Signum-Funktion.
Betragsfunktion, 
ist im Punkt 
nicht differenzierbar,
da links- und rechtsseitige Ableitung unterschiedlich sind (
bzw.
). Sie ist jedoch an dieser Stelle stetig!
Wurzelfunktion, 
ist im Punkt 
nicht differenzierbar,
da die Steigung nicht endlich ist (die Tangente verläuft senkrecht
zur x-Achse).
Ist 
in jedem Punkt des Definitionsbereiches D
differenzierbar, so heißt sie differenzierbar.
Differenzierbare Funktionen sind:
, 
, 
, 
, 
und alle
algebraischen Ausdrücke davon.
Die Funktion 
heißt Ableitungsfunktion
von 
.
Der Definitionsbereich D von 
ist gleich dem von 
, falls 
in ganz D differenzierbar ist.
|
|
|
|
|
|
|
|
