|
|
|
|
|
|
|
|
Vertauschbarkeit von Differentiation und Grenzprozeß:
Jede Potenzreihe darf im Innern ihres Konvergenzbereiches gliedweise
differenziert werden:
Die entstehende Potenzreihe hat denselben Konvergenzradius wie die
ursprüngliche Potenzreihe.
Gliedweise Integration:
Konvergiert die Potenzreihe
mit einem Konvergenzradius r, so konvergiert auch die Reihe
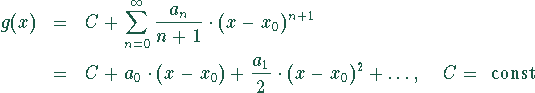
und zwar mit dem gleichen Konvergenzradius r.
Addition, Subtraktion, Multiplikation von zwei (oder mehr)
Potenzreihen im gemeinsamen Konvergenzbereich ist gliedweise möglich.
Konvergenz der Summe, der Differenz, des Produktes mindestens im
gemeinsamen Konvergenzbereich.
Stetigkeit: Eine Potenzreihe ist (zumindest) im Inneren ihres
Konvergenzbereiches stetig.
Identitätssatz:
Sind die Grenzwerte zweier Potenzreihen gleich
für 
,
wobei r das Minimum der beiden Konvergenzradien ist, dann sind auch alle Ableitungen gleich,
Damit folgt die Gleichheit der Koeffizienten 
und 
,
wenn 
gesetzt wird,
Darstellung einer Funktion: Wird eine Funktion durch eine
Potenzreihe dargestellt, dann ist die Potenzreihe die
Taylor-Reihe zum Entwicklungspunkt.
|
|
|
|
|
|
|
|
