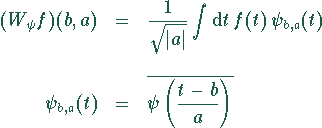
|
|
|
|
|
|
|
|
für 
. Der Parameter b gibt den Ort, a die
Skala (Ausdehnung) der Basisfunktion 
an. Die Funktion
heißt Wavelet (kleine lokalisierte Welle), wenn es möglich ist, aus 
wieder die ursprüngliche Funktion 
zu berechnen:
mit einer vom Wavelet abhängigen Konstante 
.
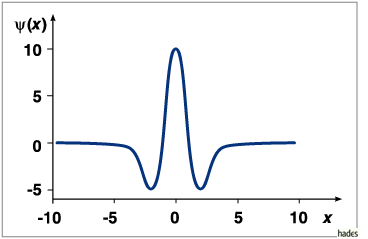
Die zweite Ableitung einer Gaußfunktion ist ein einfaches
Wavelet
Die Wavelet-Transformation ist eine lineare Signalanalyse, deren Basis
durch Translation und Dilatation aus einer einzigen Funktion 
, dem
Wavelet, erzeugt werden kann.
Die allgemeine Wavelet-Basis ist übervollständig. Es ist daher nur
nötig, den Wert von 
bei bestimmten Werten von a und
b zu kennen. Man erreicht das, indem man die Zeit-Frequenz-Darstellung
in gleich große Rechtecke entsprechend der Unschärferelation unterteilt.
|
|
|
|
|
|
|
|
