|
|
|
|
|
|
|
|
auf Eins setzt. Die rekonstruierte Signalfunktion zu diesem
Koeffizientenvektor ist gerade das Wavelet.
Signalkompression mit Wavelets: Anstelle das gesamte Signal zu übertragen,
überträgt man nur die (nach dem Absolutbetrag) größten
Waveletkoeffizienten des Signals. Bereits 10% der Koeffizienten genügen
bei vielen Signalen, um eine ausreichende Darstellung des Signals zu
erhalten. Praktische Anwendungen sind die Kompression von Video- und
Audioinformationen.
Numerik mit Wavelets: Bei der numerischen Lösung von Integral- und
Differentialgleichungen sind Wavelets oft besser geeignet als die Orts-
oder Frequenzdarstellung, weil sie sich den Spitzen und Zacken, die in
nichtlinearen Systemen auftreten, anpassen können. Ein verwandtes
Verfahren ist das Multigrid, bei dem die Gittergröße dem Verhalten
der Funktion angepaßt wird. Datenkompression mit Wavelets. Das weiter vorn dargestellte Foto mit den 5%, 2% bzw. 1% höchsten Koeffizienten.
|
|
|
|
|
|
|
|
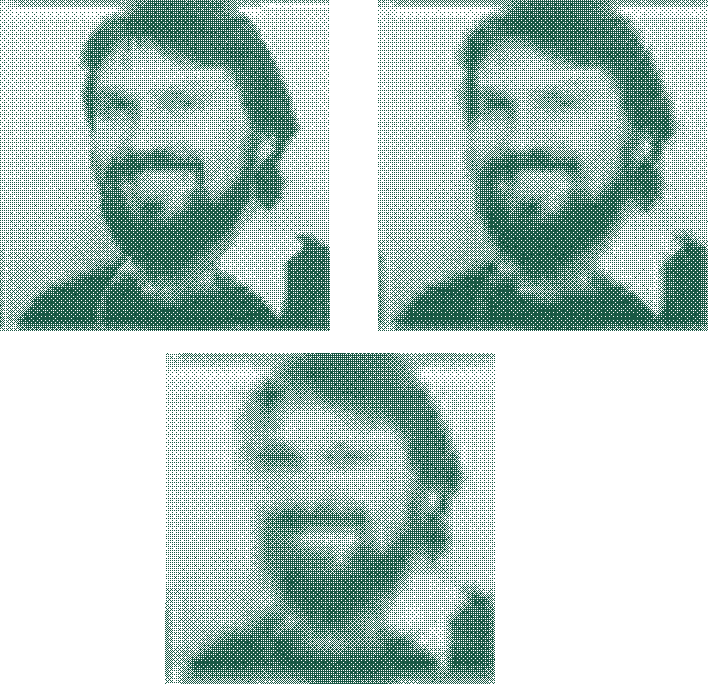
