|
|
|
|
|
|
|
|
Fourier-Reihe der 
-periodischen Funktion
auf 
, wobei 
das
Grundperiodizitätsintervall
ist und abkürzend für 
steht.
Die Funktion läßt sich damit für alle t bestimmen, indem die
Funktion auf diesem
Grundintervall einfach 
-periodisch wiederholt wird. Ein Beispiel einer
Fourier-Reihe ist die Sägezahnfunktion,
d.h.: 
und 
für 
.
Die Fourier-Koeffizienten von 
-periodischen Funktionen
folgen aus der Orthogonalität der trigonometrischen Funktionen
auf dem Intervall 
:
Hierbei ist 
das Kroneckersymbol mit 
für 
und 
für 
.
Berechnung der Orthogonalität der Sinusfunktion auf dem
Intervall 
. Für das Produkt der beiden Sinusfunktionen
gilt die trigonometrische Formel:
Diese Zerlegung kann in das Integral eingesetzt werden:
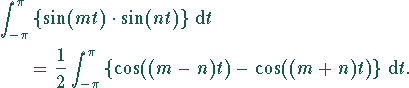
Nun muß eine Fallunterscheidung vorgenommen werden:
Fall 1: 
:
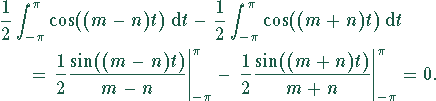
Fall 2: 
:
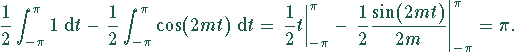
Aus diesen beiden Fällen folgt unmittelbar die Orthogonalität der Sinusfunktion.
|
|
|
|
|
|
|
|
