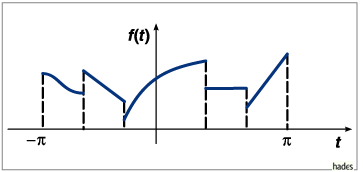
|
|
|
|
|
|
|
|
Zur Dirichletschen Bedingung a): Eine auf endlich vielen Teilintervallen stetige und monotone Funktion
in endlich viele
Teilintervalle, auf denen 
stetig und monoton ist.
gilt:
(linksseitiger Grenzwert) und
(rechtsseitiger Grenzwert) existieren.
An der Sprungstelle
ist die Fourier-Reihe der Mittelwert aus links- und rechtsseitigem Grenzwert
Besselsche Ungleichung, die Summe der Quadrate der
ersten N Koeffizienten der Fourier-Reihe ist nach oben beschränkt:
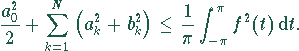
Die Differenz der beiden Terme stellt das mittlere Fehlerquadrat
zwischen der Funktion 
und ihrer Approximation durch
trigonometrische Funktionen dar. Aus dieser Ungleichung folgt daher,
daß das mittlere Fehlerquadrat positiv oder Null ist.
Parsevalsche Gleichung,
Grenzwert (
) der Besselschen
Ungleichung:
Für den Fall, daß die Funktion 
durch eine
Fourier-Reihe dargestellt werden kann, verschwindet
das mittlere Fehlerquadrat (s.o.) im Grenzübergang 
.
|
|
|
|
|
|
|
|
