Faltungssatz
Die Laplace-Transformierte der Faltung
zweier Originalfunktionen 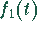 und
und  ist gleich dem Produkt der
Laplace-Transformierten dieser beiden Originalfunktionen:
ist gleich dem Produkt der
Laplace-Transformierten dieser beiden Originalfunktionen:

 In der Praxis wird der Faltungssatz benutzt, um aus einer
Bildfunktion
In der Praxis wird der Faltungssatz benutzt, um aus einer
Bildfunktion  , die sich im Bildbereich
in zwei Funktionen faktorisieren läßt,
, die sich im Bildbereich
in zwei Funktionen faktorisieren läßt, 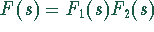 , die
Originalfunktion zu bestimmen. Das führt zu der folgenden Prozedur:
, die
Originalfunktion zu bestimmen. Das führt zu der folgenden Prozedur:
- Faktorisieren der Bildfunktion:
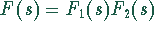 .
.
- Aufsuchen der Originalfunktionen
 und
und 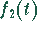 der
Bildfunktionen
der
Bildfunktionen  und
und 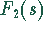 mit Hilfe der
Transformationstabelle.
mit Hilfe der
Transformationstabelle.
- Die Faltung von
 mit
mit 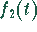 im Originalbereich ergibt
die gesuchte Originalfunktion,
im Originalbereich ergibt
die gesuchte Originalfunktion,  ,
die zu der Bildfunktion
,
die zu der Bildfunktion 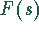 gehört.
gehört.
 Bestimmen der Originalfunktion
Bestimmen der Originalfunktion 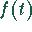 , die zur Bildfunktion
, die zur Bildfunktion

gehört.
- Die Zerlegung von
 in
in 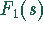 und
und
 ergibt:
ergibt:

- Mit Hilfe der Transformationstabelle findet man für die
Originalfunktionen
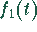 und
und  :
:

und

- Die gesuchte Lösung ist die Faltung von
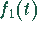 und
und
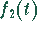 :
:
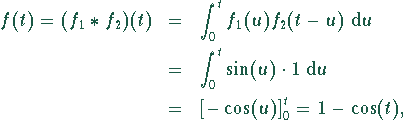
d.h., die gesuchte, zur Bildfunktion  gehörende Originalfunktion
ist
gehörende Originalfunktion
ist  .
.















![]()
 In der Praxis wird der Faltungssatz benutzt, um aus einer
Bildfunktion
In der Praxis wird der Faltungssatz benutzt, um aus einer
Bildfunktion ![]() , die sich im Bildbereich
in zwei Funktionen faktorisieren läßt,
, die sich im Bildbereich
in zwei Funktionen faktorisieren läßt, ![]() , die
Originalfunktion zu bestimmen. Das führt zu der folgenden Prozedur:
, die
Originalfunktion zu bestimmen. Das führt zu der folgenden Prozedur:
 Bestimmen der Originalfunktion
Bestimmen der Originalfunktion ![]()
![]()
![]()
![]()
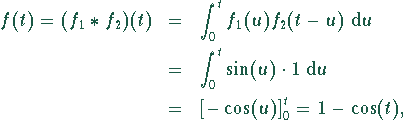
![]() gehörende Originalfunktion
ist
gehörende Originalfunktion
ist ![]() .
.







