|
|
|
|
|
|
|
|
und 
,
wobei die zweite Originalfunktion 
zeitlich verschoben ist:
Dieses Integral wird als Faltungsintegral,
Faltung oder Faltungsprodukt bezeichnet. Symbolischen
Schreibweise 
.
Diese Definition der Faltung unterscheidet
sich von derjenigen bei den
Fourierintegralen getroffenen durch die Wahl der Integrationsgrenzen,
die dort 
und 
sind.
Die Faltung ist wie ein Produkt kommutativ,
assoziativ und distributiv, daher wird auch die Bezeichnung
Faltungsprodukt verwendet.
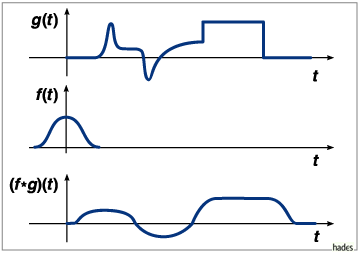
Faltung am Beispiel zweier Funktionen
|
|
|
|
|
|
|
|
