Verschiebungssatz für Verschiebung nach links
Die Laplace-Transformierte einer um die Zeit a nach links
verschobenen Originalfunktion ist gleich der Differenz zwischen der
Laplace-Transformierten der nichtverschobenen Funktion und dem
Integral 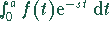 , wobei die Differenz mit dem
Faktor
, wobei die Differenz mit dem
Faktor  zu multiplizieren ist:
zu multiplizieren ist:
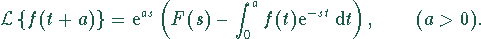
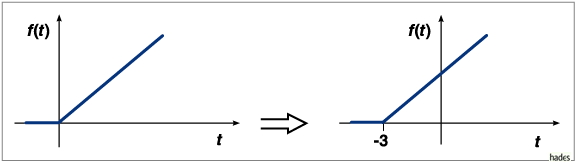
Nach links verschobene Gerade
 Laplace-Transformierte der um 3 Einheiten nach links
verschobenen Funktion
Laplace-Transformierte der um 3 Einheiten nach links
verschobenen Funktion 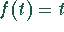 , die die Laplace-Transformierte
, die die Laplace-Transformierte 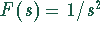 (s. Transformationstabelle) hat. Mit dem Verschiebungssatz
für Verschiebungen nach links folgt:
(s. Transformationstabelle) hat. Mit dem Verschiebungssatz
für Verschiebungen nach links folgt:
















![]()

 Laplace-Transformierte der um 3 Einheiten nach links
verschobenen Funktion
Laplace-Transformierte der um 3 Einheiten nach links
verschobenen Funktion ![]() , die die Laplace-Transformierte
, die die Laplace-Transformierte ![]() (s. Transformationstabelle) hat. Mit dem Verschiebungssatz
für Verschiebungen nach links folgt:
(s. Transformationstabelle) hat. Mit dem Verschiebungssatz
für Verschiebungen nach links folgt:








