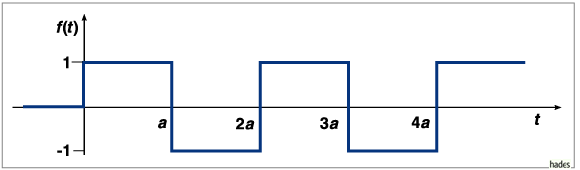
|
|
|
|
|
|
|
|
Die Laplace-Transformierte der Rechteckfunktion
mit der Periode 
soll berechnet werden. Mit dem Satz für periodische Funktionen
erhält man:
Das erste Integral liefert:
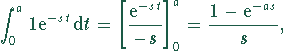
analog ergibt das zweite Integral:
Damit folgt für 
:
Zähler und Nenner lassen sich als Binome darstellen, und zwar der
Zähler als 
und der Nenner als
. Damit nimmt die Laplace-Transformierte der
Rechteckfunktion die folgende Form an:
|
|
|
|
|
|
|
|
