|
|
|
|
|
|
|
|
Gesucht: das Weg-Zeit-Gesetz der Masse in dem im Aufzug verankerten Bezugssystem.
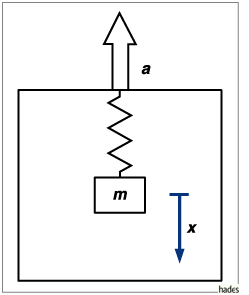
Eine an einer Feder befestigte Masse wird mit einem Aufzug nach oben beschleunigt
Die Newtonsche Bewegungsgleichung liefert eine lineare Differentialgleichung 2. Ordnung mit konstanten Koeffizienten:
mit der Einheitssprungfunktion 
. Umformung ergibt:
Die Feder gehorcht dem Hookeschen Gesetz mit der Federkonstanten k.
Die Kreisfrequenz ist 
.
Anfangsbedingung: Zur Zeit 
soll
die Masse nicht ausgelenkt sein und sich nicht bewegen:
.
Die Lösung wird mit Hilfe der Laplace-Transformation in drei Schritten ermittelt:
1. Transformation vom Original- in den Bildbereich:
2. Algebraische Lösung der Differentialgleichung im Bildbereich:
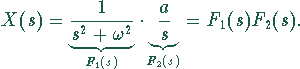
3. Rücktransformation vom Bild- in den Originalbereich:
ist das Produkt der zwei Bildbereichsfunktionen 
und
: Zur Lösung kann der Faltungssatz herangezogen werden. Dazu
müssen die zu 
und 
gehörigen Originalfunktionen
und 
anhand der Transformationstabellen bestimmt
werden:
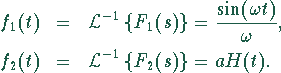
Die gesuchte Lösung im Originalbereich ist nach dem Faltungssatz das
Faltungsprodukt von 
und 
:
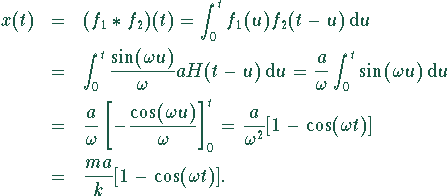
Die Lösung 
beschreibt eine harmonische Schwingung der Feder mit der
maximalen Auslenkung 
.
Die Auslenkung 
der Masse m als
Funktion der Zeit
|
|
|
|
|
|
|
|
