|
|
|
|
|
|
|
|
in einem Gefäß mit der
Grundfläche A und mit Zufluß und Abfluß berechnet
werden. Der Zufluß soll gegeben sein durch 
und der
Abfluß durch 
, wobei w und k Proportionalitätskonstanten
sind. Die Massenerhaltung führt auf eine lineare Differentialgleichung
1. Ordnung für die Wasserhöhe 
.
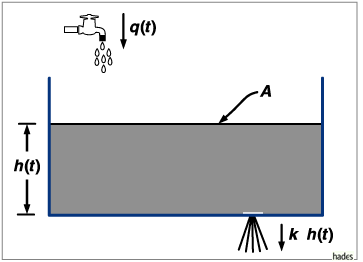
Ein Wasserbehälter mit Zu- und Abfluß
Die Anfangsbedingung ist: 
m. Die Zahlenwerte für die
Konstanten sind:
Die Lösung erfolgt mit Hilfe der Laplace-Transformation in drei Schritten:
1. Transformation der Differentialgleichung in den Bildbereich:
mit Zahlenwerten:
2. Algebraische Lösung im Bildbereich:
woraus 
folgt:
Für 
muß eine Partialbruchzerlegung durchgeführt werden:
Zur Berechnung von A wird diese Gleichung mit 
multipliziert
und 
gesetzt:
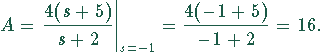
Entsprechend erhält man für B:
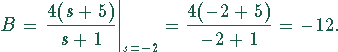
hat also die Form:
3. Rücktransformation in den Originalbereich mit Hilfe der Transformationstabellen:
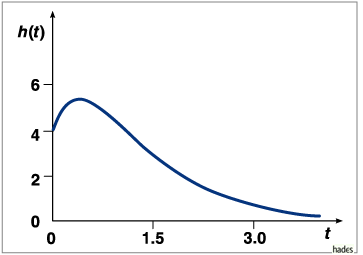
Die Wasserhöhe 
in dem Behälter als Funktion
der Zeit
|
|
|
|
|
|
|
|
