|
|
|
|
|
|
|
|
berechnet werden.
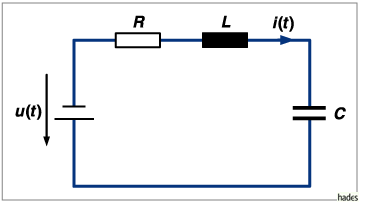
Die Anfangsbedingungen sind 
und
. Der Stromkreis wird durch die Differentialgleichung
beschrieben. Die Konstanten sind die Induktivität 
H,
der Widerstand 
und die Kapazität 
F. Die angelegte
Spannung soll linear mit der Zeit ansteigen:
Damit wird die Differentialgleichung zu:
Die Lösung erfolgt wieder mit Hilfe der Laplace-Transformation in drei Schritten:
1. Transformation in den Bildbereich:
2. Lösen der algebraischen Gleichung im Bildbereich:
Zur Bestimmung der Originalfunktion 
muß eine
Partialbruchzerlegung für 
durchgeführt werden. Dazu müssen
zuerst die Nullstellen der quadratischen Form berechnet werden:
Mit Hilfe der p-q-Formel findet man die beiden komplex konjugierten Nullstellen
Damit ist die Partialbruchzerlegung
Zu berechnen sind die Koeffizienten A, B und C. A erhält man
durch Multiplikation obiger Gleichung mit s und durch die Wahl
:
Zur Berechnung von B wird mit 
multipliziert und
gesetzt:
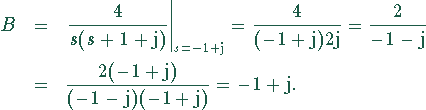
Jede komplexe Zahl 
kann in Polarkoordinatenform
geschrieben werden: 
mit dem Betrag der komplexen
Zahl 
und dem Polarwinkel 
in der
komplexen Ebene. B wird in Polarkoordinaten zu
Entsprechend ergibt sich C aus der Multiplikation mit 
und
der Wahl von 
:
also das komplex konjugierte von B.
Damit wird 
zu:
3. Mit Hilfe der Transformationstabellen wird aus der Bildfunktion
die Originalfunktion 
ermittelt:
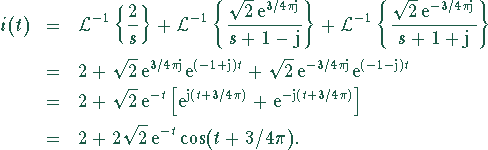
Hierbei wurde die Eulersche Relation im letzten Schritt benutzt.
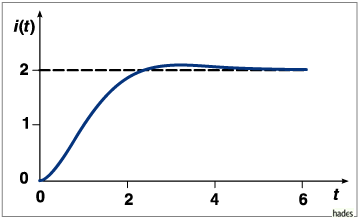
Der Strom 
als Funktion der Zeit
|
|
|
|
|
|
|
|
