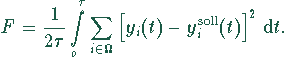
|
|
|
|
|
|
|
|
Auch die Ziel-Signale sind natürlich zeitabhängig angegeben;
ist die Länge des betrachteten Zeitintervalls.
Gewichts-Änderungen erhält man durch Integration:
Fehler-Signale eines zeitabhängigen Systems werden (wie die Signale) durch (numerische) Lösung von Differentialgleichungen berechnet:
stets mit den Randbedingungen 
.
Für Ausgabe-Knoten ist 
,
für alle anderen Knoten gilt 
.
Nach der Vorwärts-Propagation der Signale findet
eine Rückwärts-Propagation der Fehler-Signale durch das Netz
und durch die Zeit statt (daher der Name des Algorithmus).
Man erhält zum Beispiel für Fehler-Signale von Ausgabe-Knoten
nach dem Euler-Verfahren die Gleichungen:
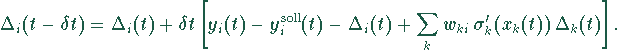
Bei Verwendung des Euler-Verfahrens für die Berechnung von
Signalen und Fehler-Signalen erhält man ein diskretisiertes Modell,
in dem die Gradientenberechnung wiederum exakt ist.
Der Lernvorgang erfolgt, abgesehen von der Zusammenfassung vieler
Zeitschritte in einzelne Muster, analog zur Standard-Backpropagation.
Für die numerische Berechnung der Fehler-Signale werden alle Signale
für jeden Zeitschritt der Vorwärts-Propagation zwischengespeichert.
Bei ausreichender Speicherkapazität ist es sinnvoll,
auch die Eingangssignale 
zu speichern.
Neben der Größe des Netzes sollte auch die Zeitskala
der jeweiligen Anwendung angepaßt werden. Am einfachsten ist es,
die Daten entsprechend zu normieren.
Zum Zeichnen einer Acht (durch ein Netz mit einer vollständig verknüpften
versteckten Schicht und mit jeweils einem Ausgabeknoten für
horizontale und vertikale Komponente) hat sich beispielsweise ein
-Intervall von 
als günstig erwiesen.
Beim Lernen komplexer Zusammenhänge kann es vorteilhaft sein,
zunächst nur einen kleinen Teil des Zeitintervalls zu berücksichtigen
und diesen dann sukzessive zu vergrößern. So werden Schwierigkeiten mit
sehr großen Fehler-Signalen nach langen Propagationen vermieden.
Alternativ bietet sich ein Teacher-Forcing-Verfahren an.
|
|
|
|
|
|
|
|
