|
|
|
|
|
|
|
|
Sei eine Gesamtmenge von
Einheiten gegeben, von denen 
besonders
markiert sind (z.B. unterschiedliche Farbe, Funktionstüchtigkeit),
so daß 
den Anteil der besonders gekennzeichneten Teile
an der Gesamtmenge angibt. Die Wahrscheinlichkeit, daß sich unter
zufällig ausgewählten Einheiten (Stichprobe)
genau k besonders markierte befinden, ist nun gerade
durch die hypergeometrische Verteilung gegeben.Nach jeder Entnahme einer Einheit kann sich der Anteil der markierten Elemente an der Grundgesamtheit ändern. Für jede der n Entnahmen gelten daher andere Wahrscheinlichkeiten, ein markiertes Element zu erhalten. Die hypergeometrische Verteilung simuliert somit das Ziehen von Losen ohne Zurücklegen des jeweils gezogenen Loses im Gegensatz zu der Binomialverteilung.
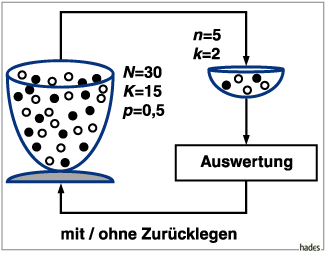
Wahrscheinlichkeit für k fehlerhafte Teile
in einer Stichprobe vom Umfang n aus einer Gesamtmenge von N Teilen,
wobei p der Anteil der fehlerhaften Stücke in der Gesamtmenge,
d.h. 
die Anzahl der fehlerhaften Teile ist.
|
|
|
|
|
|
|
|
