|
|
|
|
|
|
|
|
) und der Umfang der
Stichprobe n klein bleibt.
Sie wird verwendet, wenn n Wiederholungen eines zufälligen Versuches
unabhängig voneinander durchgeführt werden und bei jeder Wiederholung
das Ereignis A mit 
und das Ereignis 
mit
eintritt (Bernoullisches Versuchsschema).
Die Binomialverteilung beschreibt daher exakt das Ziehen von Losen aus einer Urne mit Zurücklegen des jeweils gezogenen Loses, die Wahrscheinlichkeit, unter n ausgewählten Einheiten genau k markierte zu finden.
Parameter der Verteilung sind der
markierte Anteil p und der Stichpro-
benumfang n.
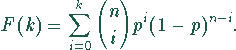
Erwartungswert: 
,
Varianz: 
.
Wesentlich ist, daß durch die Entnahme einer Einheit die Wahrscheinlichkeit,
eine markierte Einheit zu ziehen, nicht (oder kaum) verändert wird.
Im Rahmen einer Ausschußprüfung mit großen Stückzahlen N
und
kleinem Stichprobenumfang n gibt die Binomialverteilung
die Wahrscheinlichkeit an, k fehlerhafte Teile
bei insgesamt n Stichproben zu erhalten.
|
|
|
|
|
|
|
|
