Berechnung der Nullstellen eines reellen Polynoms

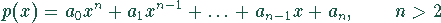
nach dem Verfahren von Bairstow bestimmt werden.

Gefundene Nullstellen werden abdividiert und das Verfahren fortgesetzt, bis eine lineare oder quadratische Gleichung übrig bleibt.

Gefundene Nullstellen sind durch Rundungs- und Abbruchfehler u.U. stark verfälscht. Deshalb muss jede Nullstelle nachiteriert werden, z.B. mit dem gewöhnlichem Newtonverfahren.

program Bairstow;

        {Berechnung der Nullstellen eines reellen Polynoms}

    const
        MaxArray = 1024; {<=32767}

    var
        n, i, deg, iter, maxit:               integer;
        r, s:                                 double; {x^2-rx-s ist ein Teiler des Polynoms}
        eps, dr, ds, eps1, eps2, x0, x1, det: double;
        abbruch:                              boolean;
        a, b, c:                              array [0..MaxArray] of double;


    procedure init; begin
        writeln('Darstellung der Berechnung der Nullstellen eines reellen');
        writeln('Polynomes mittels des Verfahren von Bairstow');
        writeln;
        writeln('Geben Sie bitte den Grad des Polynoms an');
        readln(n);
        for i:=0 to n do begin
            writeln('Geben Sie nun den Koeffizienten a[',i,'] an');
            readln(a[i]);
        end; {for}
        writeln('Wie genau sollen die Nullstellen berechnet werden?');
        readln(eps);
        while eps <= 0 do begin
            writeln('Nur positive Genauigkeiten machen Sinn. Versuchen Sie es noch einmal.');
            readln(eps);
        end; {while}
        writeln('Wieviele Iterationen sollen maximal durchgefuehrt werden?');
            readln(maxit);
        while maxit <= 0 do begin
            writeln('Nur positive Werte sind hier vernuenftig. Versuchen Sie es noch einmal.');
            readln(maxit);
        end; {while}
        deg := n;
        iter := 0;
    end {init};

    procedure loese; begin
        if sqr(r/2)<-s then begin
            writeln('Das Polynom hat komplexe Wurzeln.');
            halt
        end else begin {if}
            x0 := r/2 - sqrt(sqr(r/2) + s);
            x1 := r/2 + sqrt(sqr(r/2) + s);
            writeln(x0:1:5);
            writeln(x1:1:5)
        end {if}
    end; {loese}

    begin {Bairstow}
        init;
        while (deg > 2) and (iter < maxit) do begin
            iter := 0;
            writeln('Geben Sie geschaetzte Koeffizienten fuer einen quadratischen Teiler des');
            writeln('Polynoms an.');
            readln(r, s);
            repeat
                iter := iter + 1;
                b[deg]   := a[deg];
                b[deg-1] := a[deg-1] + r*b[deg];
                c[deg]   := b[deg];
                c[deg-1] := b[deg-1] + r*c[deg];
                i := deg - 2;
                while i>-1 do begin
                    b[i] := a[i] + r*b[i+1] + s*b[i+2];
                    c[i] := b[i] + r*c[i+1] + s*c[i+2];
                    i := i-1
                end; {while}
                det     := sqr(c[2]) - c[3]*c[1];
                abbruch := (det=0) or (iter>maxit);
                if not abbruch then begin
                    dr   := (-b[1]*c[2] + b[0]*c[3])/det;
                    ds   := (-b[0]*c[2] + b[1]*c[1])/det;
                    eps1 := dr;
                    eps2 := ds;
                    r    := r + dr;
                    s    := s + ds;
                end; {if}
            until (eps1<eps) and (eps2<eps) or abbruch;
            if not abbruch then begin
                loese;
                deg := deg - 2;
                for i:=1 to deg do begin
                    a[i] := b[i+2]
                end; {for}
            end; {if}
        end; {while}
        if (iter < maxit) then begin
            if deg=2 then begin
                r := a[1]/a[2];
                s := a[0]/a[2];
                loese
            end else begin {if}
                writeln(-a[0]/a[1]);
            end; {if}
        end else begin {if}
            writeln('Es werden zu viele Schritte benoetigt.')
        end; {if}
    end. {Bairstow}