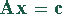Gauß-Seidel-Verfahren

program GaussSeidel(input, output);

        {Loesung des Gleichungssystems Ax = c nach dem Gauss-Seidel
        Iterationverfahren mit dem Relaxationsparameter lambda}

    uses
        stdfile;

    const MaxArray = 32; {<= 32767}

    var
        i, j, k, n:           integer;
        maxit, iter:          integer;
        a:                    array [0..MaxArray, 0..MaxArray] of double;
        c, x:                 array [0..MaxArray] of double;
        eps, dummy, sum, old: double;
        lambda, epsa:         double;


    procedure init;
        var
            fName: string;
            f:     text;
            t:     double;
        begin {init}
            writeln('Darstellung der Loesung des Gleichungssystems Ax = c nach dem');
            writeln('Gauss-Seidel-Iterationsverfahren');
            writeln;
            writeln('In welcher Datei liegen die Daten? (In gau_sei.dat liegt ein Beispiel.)');
            readln(fName);
            if StdOpen(f, fName) then begin
                if not StdRead(f, t) then begin
                    writeln('Konnte Dimension nicht lesen.');
                end; {if}
                n := round(t);
                if n > MaxArray then begin
                    writeln('Die Dimension ueberschreitet die vorgegebene Arraygroesse.');
                    halt
                end; {if}
                for i:=0 to n-1 do begin
                    if not StdReadn(f, n, @a[i, 0]) then begin
                        writeln('Konnte ', i+1, '-te Zeile nicht lesen.');
                    end; {if}
                end; {for}
                if not StdReadn(f, n, @c[0]) then begin
                    writeln('Konnte den Vektor nicht lesen.');
                end; {if}
            end else begin {if}
                writeln('Kann Datei "', fName, '" nicht oeffnen.');
                halt
            end; {if}
            close(f);
            writeln('Geben Sie bitte die gewuenschte Genauigkeit an.');
            readln(eps);
            writeln('Wie oft soll hoechstens iteriert werden?');
            readln(maxit);
            writeln('Geben Sie nun noch den Relaxationsparameter an.');
            readln(lambda);
        end; {init}

    procedure result; begin
        for i:=0 to n-1 do begin
            writeln(x[i]:8:3);
        end; {for}
    end;{result}

    begin {Gauss-Seidel}
        init;
        for i:=0 to n-1 do begin
            dummy := a[i, i];
            for j:=0 to n-1 do begin
                a[i, j] := a[i, j]/dummy;
            end; {for}
            c[i] := c[i]/dummy;
        end; {for}
        iter := 0;
        repeat
            iter := iter + 1;
            for i:=0 to n-1 do begin
                old := x[i];
                sum := c[i];
                for j:=0 to n-1 do begin
                    if i<>j then begin
                        sum := sum - a[i, j]*x[j];
                    end; {if}
                end; {do}
                x[i] := lambda*sum + (1 - lambda)*old;
                if x[i]<>0.0 then begin
                    epsa := abs((x[i] - old)/x[i]);
                end; {if}
            end; {do}
        until (iter > maxit) or (epsa < eps);
        result
    end. {Gauss-Seidel}

  Relaxationsparameter, 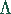 mit 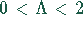, kann die Konvergenz des Gauß-Seidel-Verfahrens wesentlich verbessern:

Unterrelaxation, 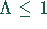, wird benutzt um nichtkonvergente Systeme zur Konvergenz zu bringen, sowie zur Dämpfung von Oszillationen, um schnellere Konvergenz zu erzielen. 

Überrelaxatio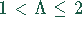n, , beschleunigt die Konvergenz bei bereits konvergenten Systemen.