Numerische Lösung von linearen Gleichungssystemen/Produktionsplanung

Zur Herstellung einer Einheit der Produkte 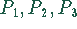werden drei verschiedene Rohstoffe 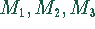mit folgenden Mengeneinheiten benötigt:

.

Wie viele Produkteinheiten 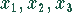können hergestellt werden, wenn folgende Masseneinheiten für die Rohstoffe zur Verfügung stehen:

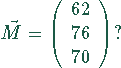
Die gesuchten Produkteinheiten bilden einen Vektor

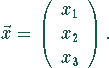
Die Tabelle der benötigten Mengeneinheiten der Rohstoffe für die einzelnen Produkte bildet eine Matrix

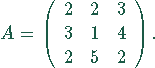
Das Gleichungssystem läßt sich dann wie folgt darstellen:

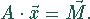
D.h.,

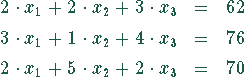
Die Lösungen erhält man durch Multiplikation mit der inversen Matrix

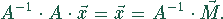
Die inverse Matrix kann nach dem Gauß-Jordan-Verfahren bestimmt werden.

Alle Umformungen, die A in die Einheitsmatrix überführen, werden gleichzeitig an der Einheitsmatrix vorgenommen. Dadurch wird diese in die inverse Matrix überführt.

1. Schritt

Die erste Gleichung wird mit 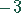und die zweite Gleichung mit multipliziert und beide Gleichungen addiert.

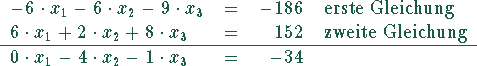
Danach zieht man die erste Gleichung von der dritten ab:

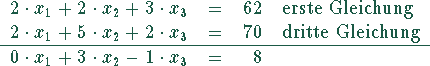
Das Ergebnis des ersten Schrittes ist

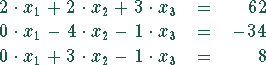
Für die Matrizen gilt:

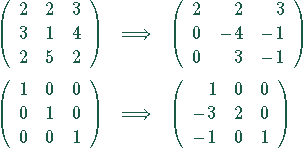
2. Schritt Elimination von 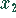außer in der zweiten Gleichung durch Multiplikation der ersten Gleichung mit mit darauffolgender Addition zur zweiten Gleichung.

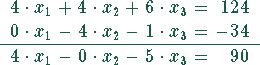
Multiplikation der zweiten Gleichung mit 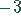, der dritten Gleichung mit 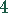und Addition beider Gleichungen:

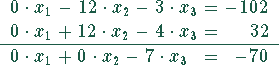
Das liefert das Gleichungssystem

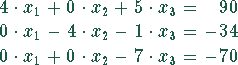
Für die Matrizen gilt:

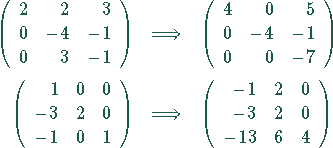
3. Schritt

Elimination von 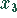aus der ersten und zweiten Gleichung.

Multplikation der ersten Gleichung mit 7, der dritten Gleichung mit 5 und darauffolgender Addition der dritten Gleichung zur ersten Gleichung:

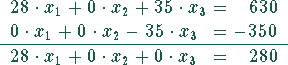
Multiplikation der zweiten Gleichung mit 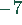und Addition der dritten Gleichung zur zweiten Gleichung:

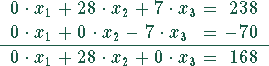
Damit erhält man folgendes Gleichungssystem

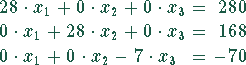
Für die Matrizen gilt:

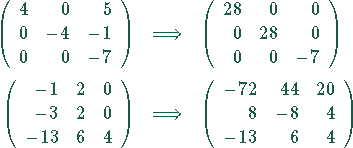
Die Matrizen werden normiert, indem die erste Zeile durch 28, die zweite Zeile durch 28 und die dritte Zeile durch 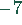geteilt werden. Das liefert die inverse Matrix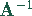

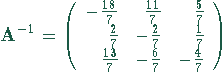
Der Vorteil der inversen Matrix ist, daß man sehr leicht auch für beliebig andere zur Verfügung stehende Rohstoffmengen die möglichen Produkteinheiten berechnen kann.

Damit ergeben sich folgende Lösungen

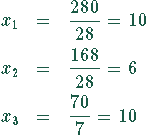
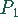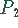Es lassen sich also 10 Produktionseinheiten des Produktes , 6 Produktionseinheiten des Produktes und 10 Produktionseinheiten des Produktes 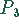herstellen.