Erste Ableitung/Grenzkostenfunktion

Die erste Ableitung einer Gesamtkostenfunktion sind die Grenzkosten. Sie geben für jeden Output x die Kostenänderung für die letzte bzw. folgende Outputeinheit an. Bestehen die Gesamtkosten aus variablen, von dem Output abhängigen Kosten, und fixen Kosten, so stimmen Grenzkostenfunktion der Gesamtkosten und der variablen Kosten überein, da der Differentialkoeffizient der konstanten fixen Kosten identisch null ist. Analog gilt für die Stückkostenfunktion .

Die Ableitung heißt die Grenz-Stückkostenfunktion. Sie gibt die Änderung der gesamten Stückkosten pro zusätzlicher Produktionseinheit an.

Die erste Ableitung einer Umsatzfunktion oder Ausgabenfunktion (x: Produktmenge; p: Preis pro Mengeneinheit) heißt die Grenzerlösfunktion. Hierbei unterscheidet man zwei Fälle:

• Die unabhängige Variable ist die nachgefragte Menge x. Dann ist die erste Ableitung der Grenzerlös bzgl. der Menge: Sie liefert die Erlösänderung, wenn sich die nachgefragte Menge um eine Einheit erhöht.

  

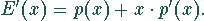
• Die unabhängige Variable ist der Preis p. Mit Hilfe der Funktion der Umkehrfunktion der Preis-Absatz-Funktion lautet die Erlösfunktion

  

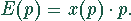
  Sie liefert die Erlösänderung, wenn der Marktpreis p des Gutes sich um eine Geldeinheit pro Mengeneinheit ändert.

  Ist eine Konsumfunktion gegeben, so liefert die erste Ableitung die marginale Konsumquote. Ihr Wert gibt zu jedem Haushaltseinkommen Y an, um wieviel Geldeinheiten sich die Konsumausgaben C dieses Haushaltes ändern, wenn das Haushaltseinkommen um eine Geldeinheit steigt.