|
|
|
|
|
|
|
|
Bedeutung: Die Steigung der Tangente (Differentialquotient) entspricht dem Grenzwert der Sekantensteigung (Differenzenquotient).
Ist die Funktion 
eine Gerade (Polynom 1. Grades),
so ist der Differenzenquotient gleich dem
Differentialquotienten.
Die Ableitung 
ist gleich
der Steigung der Geraden 
.
Näherung der Tangente durch die Sekante ist
Grundlage der numerischen Differentiation und exakt für
lineare Funktionen.
Schreibweisen für die Ableitung an der Stelle 
:
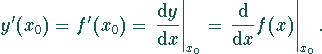
Ableitungen nach der Zeit t werden häufig durch einen Punkt anstelle des Strichs gekennzeichnet:
Die Ableitung ist punktweise definiert. Der Wert der
Ableitung hängt von der Stelle ab, an der man ableitet.
Somit stellt die Ableitung wieder eine Funktion dar.
Geschwindigkeit als Ableitung des Weges x nach der Zeit: 
,
Beschleunigung als Ableitung der Geschwindigkeit
v nach der Zeit: 
,
Strom als zeitliche Änderung der Ladung q: 
,
Steigung einer Straße,
Kraft als Ableitung des Potentiales nach dem Ort,
Minimierungs- und Maximierungsprobleme.
|
|
|
|
|
|
|
|
