|
|
|
|
|
|
|
|
Es soll eine Weißblechdose mit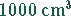 
Inhalt hergestellt werden, wobei der
Materialeinsatz ein Minimum sein soll. Dies ist eine Extremwertaufgabe für eine
Funktion mit zwei Variablen (Höhe und Radius) mit einer Nebenbedingung.
Die mathematische Formulierung dieser Extremwertaufgabe lautet
unter der Nebenbedingung
Zur Lösung wird die Lagrangesche Multiplikationsregel verwendet: Man betrachtet die Funktion
mit einem unbekannten konstanten Multiplikator und setzt deren partielle Ableitungen null:
Aus (2) folgt
Nach Einsetzen von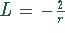 
in (0.1) ergibt sich
Dies wird in (3) eingesetzt, womit
folgt.
Damit kann die minimale Oberfläche berechnet werden.
