|
|
|
|
|
|
|
|
Unter einer Marginalanalyse versteht man die Untersuchung des Verhaltens einer ökonomischen Funktion bei sehr kleinen Änderungen der unabhängigen Variablen. Ein Beispiel ist die Änderung einer Kostenfunktion bei einer kleinen Änderung der Produktionsmenge. Wird z.B. die Abhängigkeit der Kostenfunktion von der Produktionsmenge durch die kubische Funktion
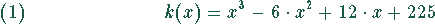
beschrieben, so lautet die Grenzkostenfunktion
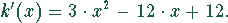
Bei einer Produktionsmenge von z.B.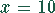 
ergibt sich als Grenzquote
Das bedeutet, bei einer Erhöhung der Produktionsmenge von 10 auf 11 Einheiten
erhöhen sich die Kosten um 192 Geldeinheiten. D.h., die Kosten steigen von
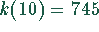auf 
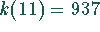Geldeinheiten. Der korrekte Wert der Kosten kann leicht aus
(1) berechnet werden:
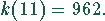
Man muß nachdrücklich bemerken, daß das Grenzverhalten eine Punkteigenschaft ist.
Trotzdem wird die Grenzänderungsquote in den Wirtschaftswissenschaften
meistens für ein endliches Intervall berechnet. Übrigens wird die relative
Abweichung der realen Kostenfunktion von den nach der Grenzänderungsquote
berechneten Kosten um so kleiner, je größer die betrachtete Produktionsmenge ist.
